基本概念
曲线与直线围成的区域面积可以通过积分与几何图形面积相结合的方法计算。
面积 = 几何图形面积 - \(\int_a^b f(x) dx\)
计算步骤
1. 找交点:确定曲线与直线的交点坐标
2. 画图:画出曲线和直线,标出交点
3. 确定积分限:根据交点确定积分的上下限
4. 计算几何面积:计算相关三角形或梯形的面积
5. 计算积分:计算曲线下的积分值
6. 求差:几何面积减去积分值得到最终面积
Example - 基础曲线与直线间面积
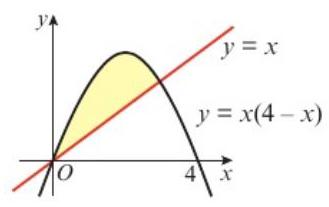
题目:Find the area of the region bounded by \(y = x(4 - x)\) and \(y = x\).
解:
交点:\(x(4 - x) = x\)
\(3x - x^2 = 0\)
\(x = 0\) 或 3
Area beneath curve = \(\int_0^3 (4x - x^2) dx = 9\)
Area beneath line = \(\int_0^3 x dx = \frac{9}{2}\)
Shaded area = \(9 - \frac{9}{2} = \frac{9}{2}\)
Example 7 - 复合图形面积
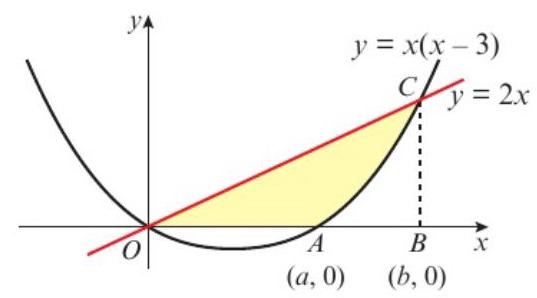
题目:Find the area of the shaded region OAC bounded by \(y = x(x - 3)\) and \(y = 2x\).
解:
交点:\(2x = x(x - 3)\)
\(x = 0\) 或 5
Area of triangle OBC = \(\frac{1}{2} \times 5 \times 10 = 25\)
Area between curve and x-axis = \(\int_3^5 x(x - 3) dx = \frac{26}{3}\)
Shaded region = \(25 - \frac{26}{3} = \frac{49}{3}\)
重要公式
三角形面积 = \(\frac{1}{2} \times 底 \times 高\)
梯形面积 = \(\frac{1}{2} \times (上底 + 下底) \times 高\)
矩形面积 = 长 × 宽
练习题精选
1. \(y = x^2 + 2\) 与 \(y = 6\) 围成的面积 = \(\frac{16}{3}\)
2. \(y = 4x - x^2\) 与 \(y = 3\) 围成的面积 = \(\frac{14}{3}\)
3. \(y = 9 - 3x - 5x^2 - x^3\) 与 \(y = 4 - 4x\) 围成的面积 = \(\frac{4}{3}\)
常见错误
• 忘记找交点
• 积分限确定错误
• 几何面积计算错误
• 符号处理错误
解题技巧
• 总是先画图
• 找交点作为积分限
• 选择合适的计算方法
• 检查答案必须为正数

